Collaborative Filtering with Embeddings

Most online ecommerce website use some kind of Recommendation engies to predict what prodcts the user would likely purchase and thus derive sales. They leverage the behavior of their previous customers: navigation, viewing, shopping history to deliver better recommendations. Collaborative filtering is a basic model for recommendation, such model is build with the assumtion that people like things similar to other things they like (if they like orange they will probably like oragne juice). Also people with similar taste would like same things.

There are different algorithms for collaborative filtering, the following implements Matrix factorization. The products of the factorizations gives the user-item ratings matrix. Then, gradient descent is used to find optimal solution (i.e. best factorization).

Data

In the following, the movie ratings dataset from Grouplens MovieLens is used. First download the data, un-compressed and have a look to the different files

$ curl -O http://files.grouplens.org/datasets/movielens/ml-20m.zip
$ unzip ml-20m.zip --directory /data/ml-20m
$ ls /data/ml-20m
genome-scores.csv  links.csv   ratings.csv  tags.csv
genome-tags.csv    movies.csv  README.txt

The ratings.csv file contains ratings, it has 20 million ratings on 27,000 movies by 138,000 users.

ratings_df = pd.read_csv(PATH+'/ratings.csv', dtype={'userId': int, 'movieId': int, 'rating': float})

In the user-item matrix, in a every cell (i, j) we will have the rating of user i on the movie j. A look into the first few rows:

    userId	movieId	rating	timestamp
0	    1	    2	3.5	    1112486027
1	    1	    29	3.5	    1112484676
2	    1	    32	3.5	    1112484819
3	    1	    47	3.5	    1112484727
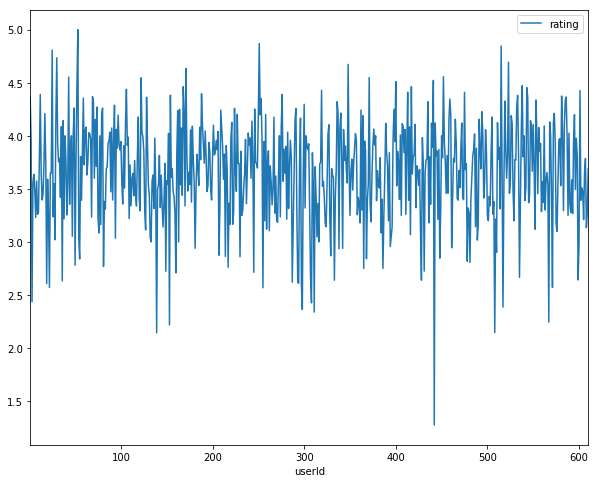
4	    1	    50	3.5	    1112484580

The following pictures depicts the distribution of ratings’ mean per movie:

Model

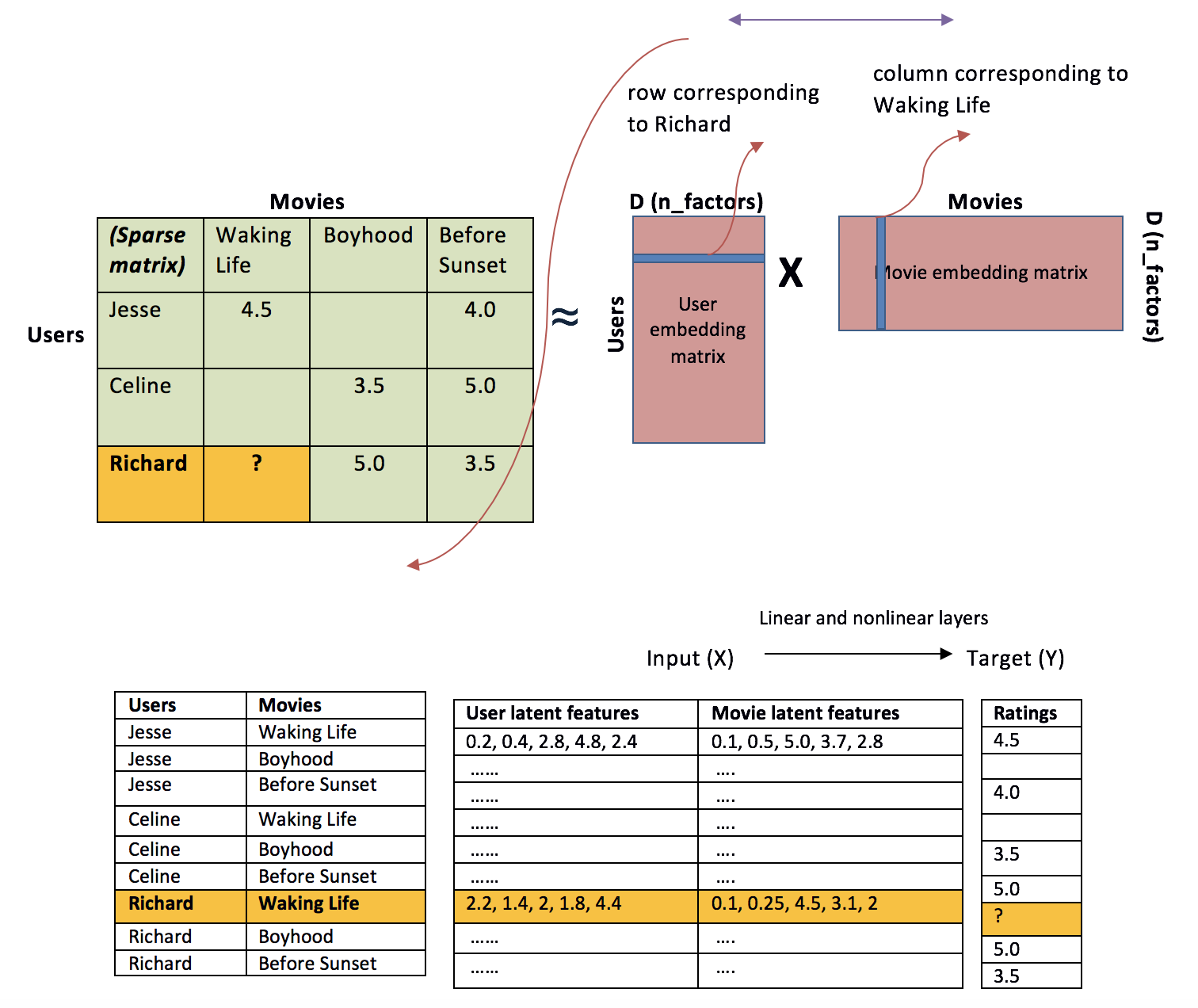
This Base model for callaborative filtering (as depicted in the picture below - source), will try to learn user-item matrix using embeddings (i.e. a matrix of weights) for users and items, the dot product should give the rating matrix. When defining the embeddings, e.g. user_embed: the number of words in vocab is the number of users we have, and the number of factors represent the dimensional embeddings.

The model also try to learn bias by user and by movie (there are movies that too many people would like or hate), and there are users who likes (or hates) every movie. Then, it applies a sigmoid function to get a probability (a value between 0 and 1), which later is scaled to the appropriate ratings and get the predicted ratings.

The model loss function is simply an Mean Squared Error (MSE), and Gradient descent (or similar) algo can be used to find optimal weights.

Here is a full Keras-based implementation:

num_factors = 5 # embedding dimentionality

# input
users_input = Input(shape=(1,))
items_input = Input(shape=(1,))

# embedding
user_weight = Embedding(num_users, num_factors, input_length=1)(users_input)
item_weight = Embedding(num_items, num_factors, input_length=1)(items_input)

# bias
user_bias = Embedding(num_users, 1, input_length=1)(users_input)
item_bias = Embedding(num_items, 1, input_length=1)(items_input)

# the collaborative filtering logic
res1 = Dot(axes=-1)([user_weight, item_weight]) # multiply users weights by items weights
res2 = Add()([res1, user_bias])                 # add user bias
res3 = Add()([res2, item_bias])                 # add item bias
res4 = Flatten()(res3)
res5 = Activation('sigmoid')(res4)              # apply sigmoid to get probabilities
# scale the probabilities to make them ratings
ratings_output = Lambda(lambda x: x * (max_score - min_score) + min_score)(res5)

model = Model(inputs=[users_input, items_input], outputs=[ratings_output])

Training

The previous snippets are grouped together into a helper class for parsing Reuters dataset.

epochs                 = 10
batch_size             = 1024
# compile the model
model.compile(loss='mean_squared_error', optimizer='adam', metrics=['accuracy'])
model.summary()
# train model
history = model.fit(
    x                = [users_train, items_train],
    y                = ratings_train,
    epochs           = epochs,
    batch_size       = batch_size,
    validation_split = 0.2,
    verbose          = 1
)

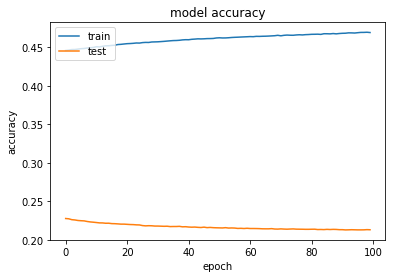
After trainning, print the history of losses and accuracy both available in the history variable.

The full jypiter notebook can be found here - link.