All things

Cloud, Data, Machine Learning, and more.

bachir | twitter

Implementing LSTM-FCN in pytorch - Part I

25 Nov 2018 by dzlab

The follwoing article implements Multivariate LSTM-FCN architecture in pytorch. For a review of other algorithms that can be used in Timeseries classification check my previous review article.

Network Architecture

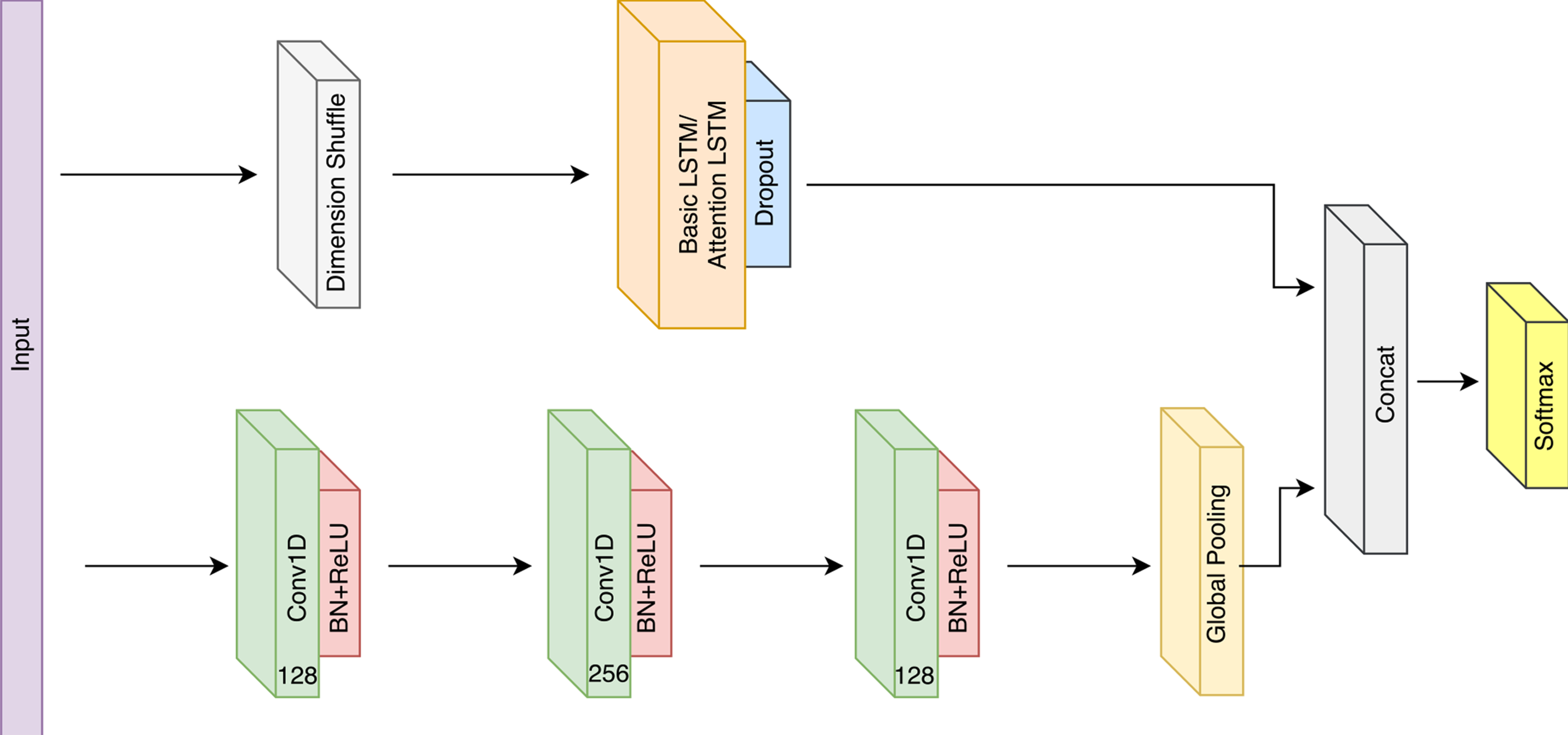
LSTM-FCN_Architecture

LSTM block

The LSTM block is composed mainly of a LSTM (alternatively Attention LSTM) layer, followed by a Dropout layer.

A shuffle layer is used at the begning of this block in case the number of time steps N (sequence length of the LSTM layer), is greater than the number of variables M.

This tricks improves the efficiency as the LSTM layer since it will require M time steps to process N variables, instead of N time steps to process M variables each timestep in case no shuffle is applied.

In pytorch, the LSRM block looks like the following:

class BlockLSTM(nn.Module):
    def __init__(self, time_steps, num_variables, lstm_hs=256, dropout=0.8, attention=False):
        super().__init__()
        self.lstm = nn.LSTM(input_size=time_steps, hidden_size=lstm_hs, num_layers=num_variables)
        self.dropout = nn.Dropout(p=dropout)
    def forward(self, x):
        # input is of the form (batch_size, num_variables, time_steps), e.g. (128, 1, 512)
        x = torch.transpose(x, 0, 1)
        # lstm layer is of the form (num_variables, batch_size, time_steps)
        x = self.lstm(x)
        # dropout layer input shape:
        y = self.dropout(x)
        # output shape is of the form ()
        return y

FCN block

The core component of fully convolutional block is a convolutional block that contains:

In pytorch, the a convolutional block looks like the following:

class BlockFCNConv(nn.Module):
    def __init__(self, in_channel=1, out_channel=128, kernel_size=8, momentum=0.99, epsilon=0.001, squeeze=False):
        super().__init__()
        self.conv = nn.Conv1d(in_channel, out_channel, kernel_size=kernel_size)
        self.batch_norm = nn.BatchNorm1d(num_features=out_channel, eps=epsilon, momentum=momentum)
        self.relu = nn.ReLU()
    def forward(self, x):
        # input (batch_size, num_variables, time_steps), e.g. (128, 1, 512)
        x = self.conv(x)
        # input (batch_size, out_channel, L_out)
        x = self.batch_norm(x)
        # same shape as input
        y = self.relu(x)
        return y

The fully convolutional block contains three of these convolutional blocks, used as a feature extractor. Then it uses a global average pooling layer to generate channel-wise statistics.

In pytorch, a FCN block would look like:

class BlockFCN(nn.Module):
    def __init__(self, time_steps, channels=[1, 128, 256, 128], kernels=[8, 5, 3], mom=0.99, eps=0.001):
        super().__init__()
        self.conv1 = BlockFCNConv(channels[0], channels[1], kernels[0], momentum=mom, epsilon=eps, squeeze=True)
        self.conv2 = BlockFCNConv(channels[1], channels[2], kernels[1], momentum=mom, epsilon=eps, squeeze=True)
        self.conv3 = BlockFCNConv(channels[2], channels[3], kernels[2], momentum=mom, epsilon=eps)
        output_size = time_steps - sum(kernels) + len(kernels)
        self.global_pooling = nn.AvgPool1d(kernel_size=output_size)
    def forward(self, x):
        x = self.conv1(x)
        x = self.conv2(x)
        x = self.conv3(x)
        # apply Global Average Pooling 1D
        y = self.global_pooling(x)
        return y

LSTM-FCN

Finally, putting together the previous blocks to construct the LSTM-FCN architecture by concatenating the out of the blocks and passing it throgh a softmax activation to generate the final output.

class LSTMFCN(nn.Module):
    def __init__(self, time_steps, num_variables):
        super().__init__()
        self.lstm_block = BlockLSTM(time_steps, num_variables)
        self.fcn_block = BlockFCN(time_steps)
        self.softmax = nn.Softmax()
    def forward(self, x):
        # input is (batch_size, time_steps), it has to be (batch_size, 1, time_steps)
        x = x.unsqueeze(1)
        # pass input through LSTM block
        x1 = self.lstm_block(x)
        # pass input through FCN block
        x2 = self.fcn_block(x)
        # concatenate blocks output
        x = torch.cat([x1, x2], 1)
        # pass through Softmax activation
        y = self.softmax(x)

Training

Part II discusses the training setup of the LSTM-FCN architecture using different Datasets.

Related Posts