Implementing LSTM-FCN in pytorch - Part II

The follwoing article continues on the training of Multivariate LSTM-FCN architecture in pytorch. Part I details the implementatin of this architecture.

Data

The dataset used for training the LSTM-FCN timeseries classifier is the Earthquake Dataset. In this classification problem we aim to predict whether a major event is about to happen based on a history of recent hourly readings taken between Dec 1st 1967, and 2003. The original sensor reading were transformed into a classification problem by:

• Definining a major event (what need to be predicted) as any reading above value 5 Rictor scale and then making sure this event is not aftershock of another major event.
• Constructing negative cases where there is a reading below 4 which was preceded by 20 or more non -zero readings in the last 512 hours.
• Segmenting the readings (rather than using a sliding window) so that they do not overlap in time.

Dowload the dataset

$ curl -O http://www.timeseriesclassification.com/Downloads/Earthquakes.zip
$ unzip Earthquakes.zip

Create pytorch DataLoaders for the training sets (should be the same for test set).

# read into numpy arrays
data_train = np.loadtxt('Earthquakes_TRAIN.txt')
X_train, y_train = data_train[:, 1:], data_train[:, 0].astype(int)
# transforms those numpy arrays into tensors
cuda = torch.device('cuda')
X_tensor = torch.tensor(X_train, dtype=torch.float32, device=device)
y_tensor = torch.tensor(y_train, dtype=torch.long, device=device)
train_ds = TensorDataset(X_tensor, y_tensor)
# pass the datasets into a DataLoader
train_dl = DataLoader(train_ds, batch_size=64, shuffle=False)

Training

Before training the previously defined pytorch model, we need to implement a learner that will use an optimization algorithm (here Adam) to update the weights (actually the gradients that will be extracted from the weights) in a way that decreases the loss as follows:

class SimpleLearner():
    def __init__(self, data, model, loss_func):
        self.data, self.model, self.loss_func = data, model, loss_func

    def update(self, x,y,lr):
        opt = optim.Adam(self.model.parameters(), lr)
        y_hat = self.model(x)
        loss = self.loss_func(y_hat, y)
        loss.backward()
        opt.step()
        opt.zero_grad()
        return loss.item()

    def fit(self, epochs=1, lr=1e-3):
        losses = []
        for i in tqdm(range(epochs)):
            for x,y in self.data[0]:
                current_loss = self.update(x, y , lr)
                losses.append(current_loss)
        return losses

As the output of the model is a hot encoded array (with number of classes as second dimension), and depending on the number of classes, we use a Binary Cross Entropy (a simple if/else statement) which is defined as follows:

For more than two classes or a Negative Log Likelihood loss which is known as Categorical Cross Entropy and is defined in a general manner by the function:

loss_func = nn.NLLLoss().cuda()

Then create the learner and train the model

learner = SimpleLearner([train_dl, test_dl], model, loss_func)
losses = learner.fit(10)

The plot of the losses over batches should look like this

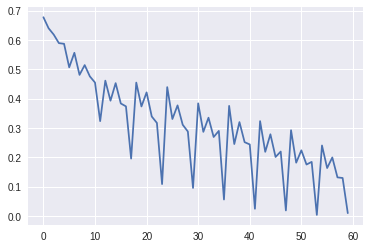
Full notebook can be found here - link